Разложение вектора на компоненты. Координаты вектора
Если  и и 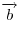 — два неколлинеарных вектора в плоскости, а — два неколлинеарных вектора в плоскости, а 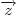 — произвольный вектор в той же плоскости, то всегда существуют такие числа — произвольный вектор в той же плоскости, то всегда существуют такие числа 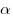 и и 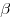 , что , что 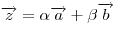 . В этом случае говорят, что вектор . В этом случае говорят, что вектор 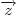 разложен по векторам разложен по векторам  и и 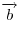 . .
Если 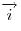 и и 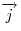 — неколлинеарные единичные векторы (т. е. вектора, модуль которых равен единице) — неколлинеарные единичные векторы (т. е. вектора, модуль которых равен единице) 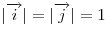 , то произвольный вектор , то произвольный вектор 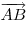 плоскости может быть представлен в виде плоскости может быть представлен в виде 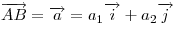 . В этом случае говорят, что вектор . В этом случае говорят, что вектор 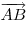 имеет в системе имеет в системе 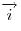 и и 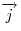 координаты координаты 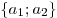 . .
Если векторы 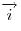 и и 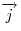 взаимно перпендикулярны, причем вектор взаимно перпендикулярны, причем вектор 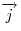 может быть получен из вектора может быть получен из вектора 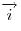 поворотом против часовой стрелки, то говорят, что прямые, в которых лежат поворотом против часовой стрелки, то говорят, что прямые, в которых лежат 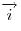 и и 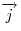 , образуют декартову прямоугольную систему координат, а числа , образуют декартову прямоугольную систему координат, а числа 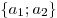 называются декартовыми координатами вектора называются декартовыми координатами вектора  . .
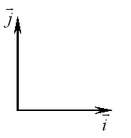
Пусть точка 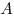 с координатами с координатами 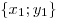 — начало вектора — начало вектора  , а точка , а точка 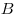 с координатами с координатами 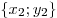 — его конец. Тогда координаты вектора связаны с координатами точек — его конец. Тогда координаты вектора связаны с координатами точек 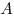 и и 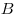 формулами: формулами:
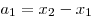 , ,
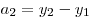 , т. е. декартовы координаты
вектора равны разности соответствующих координат конца вектора и его
начала. , т. е. декартовы координаты
вектора равны разности соответствующих координат конца вектора и его
начала.
Декартовы координаты вектора  являются проекциями
этого вектора на соответственные оси систем координат: являются проекциями
этого вектора на соответственные оси систем координат: 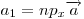 , , 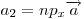 . .
Пусть вектор  имеет координаты имеет координаты 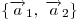 , что записывается в виде , что записывается в виде 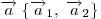 , а вектор , а вектор 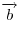 — — 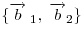 , или , или 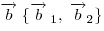 . .
Тогда:
 , ,
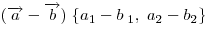 , ,
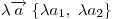 , ,
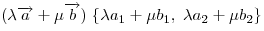 , ,
т. е. действиям с векторами отвечают идентичные действия с их координатами.
Модуль вектора  определяется через его
декартовы координаты посредством равенства: определяется через его
декартовы координаты посредством равенства: 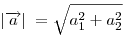 , а единичный вектор , а единичный вектор 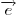 , имеющий
с вектором , имеющий
с вектором  одинаковое направление, записывается в
виде одинаковое направление, записывается в
виде  и имеет
координаты: и имеет
координаты: 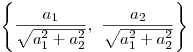 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
