Сумма и разность векторов
Два вектора складываются по правилу параллелограмма. Для этого
оба вектора откладываются из одной точки и строится параллелограмм, сторонами которого являются вектора.
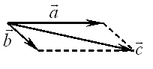
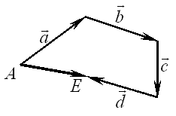
Чтобы получить сумму большего числа векторов, нужно отложить от
произвольной точки 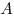 первый вектор первый вектор  , а каждый последующий вектор ( , а каждый последующий вектор (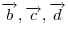 ...) отложить от конца предыдущего. Суммой будет вектор, начало которого совпадает с началом (точка ...) отложить от конца предыдущего. Суммой будет вектор, начало которого совпадает с началом (точка 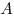 ), а конец — с концом (точка ), а конец — с концом (точка  ) последнего вектора. ) последнего вектора.
Разностью двух векторов  и и 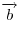 называется такой вектор называется такой вектор 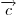 , который будучи сложенным с вектором , который будучи сложенным с вектором 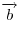 , даст , даст  . Разность двух векторов . Разность двух векторов 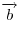 и и  представляется
направленным отрезком, соединяющим концы этих векторов и имеющим
направление «к концу того вектора, из которого вычитают». представляется
направленным отрезком, соединяющим концы этих векторов и имеющим
направление «к концу того вектора, из которого вычитают».
Если для вектора 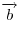 ввести противоположный ему вектор ввести противоположный ему вектор 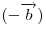 , который коллинеарен вектору , который коллинеарен вектору
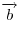 , имеет тот же модуль, но направлен в противоположную сторону, то разность векторов , имеет тот же модуль, но направлен в противоположную сторону, то разность векторов  и и 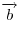 представляется как сумма вектора представляется как сумма вектора  и вектора и вектора 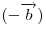 , т. е. , т. е. 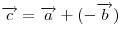 . .
Сумма противоположных векторов равна нулю: 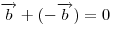 . .
Под произведением 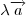 вектора вектора  на число на число 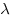 понимается такой вектор, который коллинеарен вектору понимается такой вектор, который коллинеарен вектору  , имеет модуль , имеет модуль  и направлен в ту же сторону, что и и направлен в ту же сторону, что и  — если — если 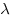 положительно, и в противоположную — если положительно, и в противоположную — если 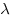 отрицательно. Геометрически умножение вектора на число означает растяжение или сжатие вектора и, возможно, перемену его направления на противоположный. отрицательно. Геометрически умножение вектора на число означает растяжение или сжатие вектора и, возможно, перемену его направления на противоположный.
Имеют место равенства:
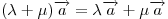 , ,
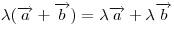 , ,
в которых 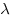 и и 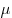 произвольные действительные числа. произвольные действительные числа.
Вектор 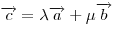 называется линейной комбинацией векторов называется линейной комбинацией векторов  и и 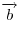 . Если . Если 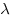 и и 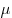 — произвольные действительные числа, а — произвольные действительные числа, а  и и 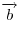 — неколлинеарные вектора, то варьируя эти числа, можно получить произвольный вектор плоскости. — неколлинеарные вектора, то варьируя эти числа, можно получить произвольный вектор плоскости.
Если 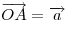 и и 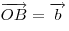 — два неколлинеарных вектора, отложенные от точки — два неколлинеарных вектора, отложенные от точки 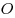 , то вектор , то вектор 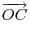 , оканчивающийся в середине отрезка , оканчивающийся в середине отрезка 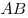 , равен полусумме векторов , равен полусумме векторов  и и 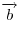 , т. е. , т. е. 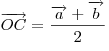 . .
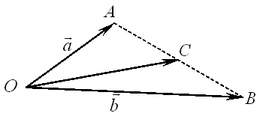
В общем случае, вектор точки 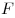 , делящий отрезок , делящий отрезок 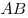 в
соотношении в
соотношении 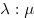 ( (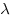 и и 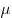 — положительные числа) и начинающийся в точке — положительные числа) и начинающийся в точке 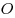 , дается формулой: , дается формулой: 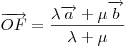 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
