Определения
Упорядоченная пара 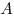 , ,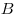 несовпадающих точек определяет направленный отрезок с началом несовпадающих точек определяет направленный отрезок с началом 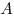 и концом и концом 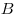 . С помощью этого отрезка задается преобразование плоскости — параллельный перенос, при котором каждая точка . С помощью этого отрезка задается преобразование плоскости — параллельный перенос, при котором каждая точка 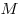 отображается на такую точку отображается на такую точку 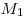 , что луч , что луч 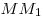 сонаправлен с лучом сонаправлен с лучом 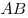 и расстояние и расстояние 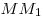 равно расстоянию равно расстоянию 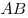 . Такое преобразование называется вектором. Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой и обозначается . Такое преобразование называется вектором. Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой и обозначается 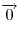 . .
Ненулевой вектор изображается направленным отрезком и обозначается символом 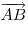 или или  . .
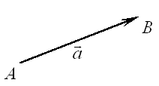
Один и тот же параллельный перенос можно задать с помощью бесконечного количества направленных отрезков. Все такие отрезки имеют одинаковую
длину, называемую длиной или модулем вектора 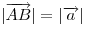 , параллельны (или лежат на одной прямой) и направлены в одну сторону. , параллельны (или лежат на одной прямой) и направлены в одну сторону.
Если векторы 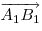 и и 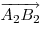 изображаются отрезками, лежащими на одной или на параллельных прямых, то они называются коллинеарными. Если векторы не являются коллинеарными, то они называются неколлинеарными. изображаются отрезками, лежащими на одной или на параллельных прямых, то они называются коллинеарными. Если векторы не являются коллинеарными, то они называются неколлинеарными.
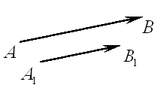
Если два ненулевых вектора  и и 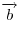 коллинеарны, то они могут быть напрвлены либо в одну сторону, либо противоположно. В первом случае вектора коллинеарны, то они могут быть напрвлены либо в одну сторону, либо противоположно. В первом случае вектора  и и 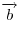 называются сонапрввленными: называются сонапрввленными: 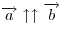 , а во втором — противоположно напрвленными: , а во втором — противоположно напрвленными: 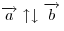 . .
Два вектора называются равными, если они сонаправлены и их длины равны.
Для каждой точки 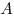 можно построить единственную точку можно построить единственную точку 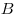 такую, что такую, что 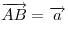 . Это
построение называется откладыванием вектора . Это
построение называется откладыванием вектора  от точки от точки 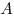 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
