Призма
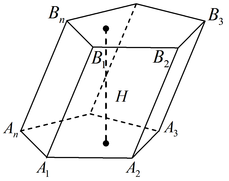
Призмой называется многогранник, две грани которого
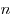 -угольники, а остальные -угольники, а остальные 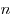 граней — параллелограммы. граней — параллелограммы.
Боковые ребра призмы, как противоположные стороны параллелограммов,
последовательно приложенных друг к другу, равны и параллельны.
Перпендикуляр, проведенный из какой-либо точки одного основания к
плоскости другого основания, называется высотой призмы. Отрезок,
соединяющий две вершины призмы, не принадлежащие одной грани,
называется диагональю призмы.
Поверхность призмы состоит из оснований и боковой
поверхности призмы. Боковая поверхность призмы состоит из
параллелограммов.
Если боковые ребра призмы перпендикулярны к основаниям, то призма
называется прямой. В противном случае призма называется
наклонной.
У прямой призмы боковые грани – прямоугольники.
Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если она прямая, и ее
основания — правильные многоугольники
Площадь поверхности и объём призмы
Пусть H — высота призмы, 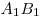 —
боковое ребро призмы, —
боковое ребро призмы, 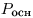 — периметр
основания призмы, — периметр
основания призмы, 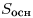 площадь основания призмы, площадь основания призмы,
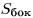 — площадь боковой поверхности призмы, — площадь боковой поверхности призмы,
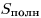 — площадь полной поверхности призмы, — площадь полной поверхности призмы, 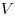 - объем призмы, - объем призмы, 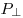 —
периметр перпендикулярного сечения призмы, —
периметр перпендикулярного сечения призмы, 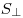 —
площадь перпендикулярного сечения призмы. Тогда имеют место следующие
соотношения: —
площадь перпендикулярного сечения призмы. Тогда имеют место следующие
соотношения:
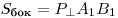

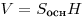
Для прямой призмы, у которой боковые ребра перпендикулярны
плоскостям оснований, площадь боковой поверхности и объем даются
формулами:
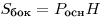
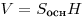
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
